Plimbare sau inspecţie

ElZap


Un parc cu alei. Ca cele din figura de mai sus. Simplu.
Dacă vreţi putem să le dăm şi nume vârfurilor dreptunghiului. A, B, C, D. Începând din coltul stânga sus. Mergem după cum merg acele ceasornicului. Putem să-i dăm centrului numele O.

Lăţimea dreptunghiului: 6 metri.
Lungimea dreptunghiului: 8 metri.
Lungimea diagonalelor? Inutil să spun. Evident 10 metri. Din cauză de Pitagora.
Câte cinci metri de fiecare parte a centrului.

Un paznic. Rolul lui? În fiecare zi să inspecteze aleile metru cu metru.Nu trebuie să lase nimic neinspectat.

El poate începe din oricare colţ. Dacă vrea poate începe şi din centru.

El ar vrea să parcurgă un traseu cât mai scurt. Nu are voie să ţopăie dintr-un colţ în altul. Poate termina oriunde.

Cam câţi metri are de inspectat paznicul zilnic?

Explicaţiile se impun.

UPDATE:
Un desen mai acătării:















REZOLVARE (PROGRESIVĂ):

R1:

Dacă o figură este formată din "insule" (ca în exemplul de mai jos) paznicul nu poate parcurge/inspecta toate aleile în niciun fel.



(De la A la E nu pot ajunge decât cu elicopterul.)
Urmează R2.





INTERMEZZO

Pentru acei copii mari sau mici care nu au obosit să se joace cu creionul pe hârtie.
Cine ştie ce drăcie mai poate ieşi din jocul ăsta?



R2:

Să presupunem de acum încolo că reţeaua de alei nu are insule ca în exemplul de mai sus, aşa că paznicul o poate inspecta fără bătaie de cap. Este şi cazul cu reţeaua din problema noastră.

Să zicem că îi cerem paznicului să facă în aşa fel încât să nu treacă de două ori pe o alee.

Dacă paznicul pleacă din intersecţia X şi termină inspecţia în intersecţia Y, o să vedem că pentru orice intersecţie Z, alta decât cele două X, Y numărul de alei ce se întâlnesc în Z este par. Asta din cauză că pe o alee a intrat şi pe una a ieşit din Z (le poate şterge din desen dacă vrea, ca să nu ne mai încurce la socoteli), şi nu a rămas nicio alee neparcursă care să fie vecină cu Z.

Pentru punctele de start şi stop X, Y, vom avea un număr impar de alei ce se întâlnesc în ele dacă ele sunt diferite, sau un număr par dacă sunt identice.

În concluzie:

Dacă numărul de intersecţii cu un număr impar de alei adiacente, este diferit de 2 sau 0, nu poate nimeni să parcurgă reţeaua trecând doar odată pe fiecare alee.

Este şi cazul reţelei noastre ce are 4 intersecţii impare. Prin urmare cade posibilitatea ca paznicul să parcurgă reţeaua în 48 de metri.

Exemplul 1



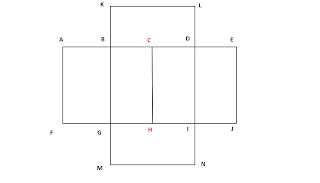
În acest exemplu aleile pot fi parcurse o singură dată, numai dacă pornim din unul din punctele C sau H.






Exemplul 2



În acest exemplu aleile pot fi parcurse o singură dată, pornind din oricare din punctele rețelei.





Exemplul 3



Nu există posibilitatea de a parcurge rețeaua o singură dată din cauză că am 4 puncte ce au un număr impar de alei adiacente.






Ar mai trebui să demonstrăm că în situaţia în care o reţea de alei are 0 sau 2 intersecţii cu un număr impar de alei care intră/ies din ele, totdeauna putem inspecta aleile trecând o singură dată pe fiecare alee. În plus, punctul de plecare se află în intersecţiile impare (dacă sunt două) sau într-o intersecţie arbitrară dacă sunt 0 intersecţii impare.

R3:



Cum rețeaua din problemă nu poate fi parcursă trecând o singură dată pe fiecare alee, caz în care paznicul ar avea de parcurs 48 de metri, suntem obligați să permitem paznicului să treacă de cel puțin două ori pe una sau mai multe alei.

Este evident că a-i permite să treacă de două ori pe o alee este echivalent cu a înlocui o alee cu două identice (a o dubla). Încercăm să dublăm aleile de 5m, 6m, 8m, ca în figura alăturată.

Dublarea aleii de 5 metri nu permite parcurgerea rețelei pentru că avem patru intersecții impare (A, C, D, O). Așadar nu putem avea un traseu de 48+5=53 metri.

Putem dubla oricare din aleile de 6 metri (o putem face în două moduri), sau de 8 metri (la fel o putem face în două moduri).

Evident, o vom alege pe cea de 6.
În acest caz obținem un traseu de 48+6=54 metri.

Răspuns corect
Paznicul trebuie să parcurgă zilnic 54 de metri.

Prima care a dat un răspuns corect, fără să ne ajute însă cu o motivație, a fost

INA.

Felicitări!

No Man's Land

ElZap

Ca să ştiu ce-i cu leanda asta, a trebuit să răsfoiesc niscaiva enciclopedii virtuale. La fel de virtuale precum sunt şi locuitorii ei.

Aş fi vrut să-i zic ţara nimănui, aşa ca să ştie omul nerodat cu anglicismele despre ce vreau să scriu. La ce ar fi folosit însă? Pe oamenii aceştia, oricum nu-i interesează ce se întâmplă sub picioarele lor, preferând starea de indivizi aerieni.

Când mă dau însă jos din enciclopedii, aflu despre ţara asta că nu e ca toate ţările. Poate nici nu mai e ţară. Mai ştii?

Par egzamplu...

În ţara asta...

... Marele Vizir niciodată nu ia hotărârile pe care taman el ar trebui să le ia, ci mai ales Padişahul. Uneori nici el.

... când Padişahului i se retrage dreptul de a hotărî, este adusă câte o „comisie de comisari” ce-i şoptesc Marelui Vizir (fără intermediari, fără martori şi fără explicaţii) ce trebuie să le ceară el supuşilor săi. Scurt. În timp ce ei cuvântează, el are dreptul să mâlcească ca un peşte.

... ocârmuirea ţării ăsteia intră periodic într-un fel de moarte clinică din care îşi revine când are ea chef. În tot acest timp nimeni nu bagă de seamă că ţara pluteşte în derivă cu cârma sfărâmată şi cu cârmaciul mort criţă.

... când guvernul se trezeşte ţara merge prost, iar când el se reîntoarce la starea lui naturală ea merge binişor spre bine. De aici a ieşit şi vorba cum că „e rău fără cârmă, dar mai rău cu dumneaei”, sau cam aşa ceva.

... în loc să fie disponibilizate guvernele producătoare de stricăciuni, sunt mătrăşiţi doar slujbaşii vinovaţi că au făcut ce le-au cerut guvernanţii.

... când e să trimitem pe cineva cu câte o treabă pe la o Înalta Poartă, se dă un concurs şi se alege cel plasat pe ultimul loc. Dacă nu se găseşte unul suficient de prost, se repetă concursul.

... numiţii aleşilor noştri, când e vorba de ţară, cumpără doar scump şi vând doar ieftin. Aşa a ajuns să avem o ţară costelivă ce duce în cârcă numiţi şi aleşi buhavi.

... pentru orice nepriceput în ale guvernării, ţara asta este un fel de cutie cu nisip (Sandbox mai pe englezeşte, ca să priceapă tot românul). Aici el se poate juca cât pofteşte de-a guvernarea, că nimeni nu-l întreabă câţi pacienţi decedaţi are la activ. De la un capăt la altul, ţara asta este un fel de lecţie de anatomie în care profesorul le arată ucenicilor un om mort, încercând să-i convingă cum că e viu şi nevătămat.

... orice chivuţă, dacă are chef poate să ajungă vizireasă cu acte în regulă, peste un minister al cărui nume şi menire sunt alese după fanteziile avute în ultimul vis al unei nopţi de vară.

Pe se întâmplă toate astea? Ne linişteşte Coşbuc:

„O, dar nu te-nspăimânta:
Nu la noi, se înţelege,
Ci-ntr-o ţară-ndepărtată
Sub pământ, pe undeva.”

În rest...

În rest ce-ar mai fi de spus. Aproape nimic, devreme ce a spus-o Coşbuc.
Dintr-o poveste

Şi acum...

... păi, acum dragii mei puteţi să mâlciţi cât poftiţi.

Eu sunt gata să ascult. Tăcerea.

Păduri

ElZap

Arde foc la Bucureşti

ElZap

Sau povestea sonoră a unui ţigan rege.

A fost odată...

ElZap


... o vreme când...

... oamenii se grăbeau alene şi aveau tot timpul să admire sumedenia de minuni care se petreceau peste tot în jurul lor.
Aşa au descoperit ei că pădurile sunt pline de privighetori grăbite să termine cuiburile pentru puii pe care peste o vreme aveau să-i cunoască, iar în privirea lor au năvălit roiurile de albine ce i-au învăţat arta războiului şi arta civilizaţiei.

... cei ce ştiau carte nu se buluceau să scrie doar pentru a ocupa un loc cât mai aproape de vârf în cine ştie ce top. Zelistul, Alexa şi alte chestii de astea nici măcar nu erau cunoscute pe timpul lor.
Din când în când, din sufletul lor se rupeau mici bucăţi, ce nu vroiau să-i însoţească pe drumul ce îi ducea în lumea de dincolo. Bucăţile astea s-au numit mai apoi scrieri.

... cum chaturile abia se descoperiseră, oamenii se mai întâlneau şi într-un fel de şedinţe de socializare, care se numeau fie şezători, fie baluri, fie taclale la o ceaşcă de cafea.
Mesajele lor nu erau doar stupide şiruri inerte de caractere ASCII sau UNICODE, ci cuvinte rostite, intonaţii cu subînţelesuri ascunse, gesturi patetice şi multe alte multe arabescuri necuprinse în călimara "Cu două guri întunecate, ca două porţi de labirint" a lui Topârceanu.

... nici profesori care să-i oblige pe tineri să înveţe versuri nu erau pe atunci. Cei ce citeau versuri, o făceau doar atunci când simţeau că se sufocă în proza vieţii de fiecare zi.

... când călcau pragul unui muzeu, curioşii o făceau doar pentru a-şi lipi obrazul de cioburile de viaţă salvate de la pieire. Prin aceste cioburi ei puteau vedea o lume care nu s-a stins de tot, ci pâlpâie în lumina difuză din spatele lor.

Cam aşa vor fi povestind oamenii de azi, ajunşi deja bunici. Vor fi povestind nepoţilor domniilor lor, ajunşi şi ei copii mari.

Poate că din poveştile astea se va naşte o nouă lume.

O lume ce va refuza a crede că dincolo de performanţă nu e mai găseşte nimic.

Frig

ElZap

La mine e frig.
Mă uit la termometru.
-12 grade Celsius.
Aflu că în zilele ce urmează o să se încălzească.
În fiecare zi temepratura o să crească cu patru grade şi o să şi scadă cu două grade.

Oare în câte zile ajungem la zero grade?

Unde ni-s meseriaşii

ElZap


Nimic nu se mai face ca pe vremuri.

Nici nu-i de mirare, dacă au ajuns toţi micro-fuhrerii sau microcefalii locali să se creadă îndreptăţiţi a picta un buchet de flori, ruinele unei mănăstiri din Messines, sau măcar nişte ponei cu zvastică pe crupă.

Nimic nu mă miră, dacă la televiziunile poporului intră spre a deveni vedete muzicale toţi afonii, toţi surdo-muţii şi mai ales toţi politicienii.

Mai nou, a fost pângărită până şi nobila meserie de jefuitor. Cu sau fără ciorap tras pe cap. Cu sau fără pistol.

Unde sunt vremurile de odinioară când priveam la televizor sau la cinematograf isprăvile lui Ronnie Biggs? Timp am avut destul de privit, că omul a reuşit să stea mult şi bine în libertate. Cam din 1963 până prin 2001, când de bună voie şi nesilit de nimeni s-a predat autorităţilor, spre veşnica laudă a poliţiei engleze.

Unde sunt vremurile când citeam prin ziare, sau auzeam pe unde auzeam de „Marele jaf comunist”, comis de bietul Ioanid, supravegheat tovărăşeşte de marele Alexandru Drăghici? Ce să-mi răcesc eu gura cu asemenea poveşti, când e plin internetul de ele (Dosare Ultrasecrete)? Ba chiar filmul poate fi găsit dacă e căutat cu atenţie.

Treaba e că în ziua de azi s-au demonetizat toate. Până şi Marile jafuri. Asta-i tristeţea mea.

Orice brunet, conaţional de-al nostru, este astăzi posesor de ciorap de intervenţie rapidă, de pistol în stare de funcţionare sau de speriat, şi nu trece zi de la Dumnezeu, fără să avem parte de o spargere. Mică, mare, ce contează? Noi ne râdem.

Să nu mai fi rămas nimic din dezastruoasa, de am ajuns să dăm pe sticlă doar găinării? Să ajungem ca pentru 300 de lei (noi ce-i drept), să-ţi ia gâtul orice nespălat? Unde am ajuns?

Unde sunt specialiştii cu gulere albe, care îţi retezau un Bancorex într-o singură noapte, de ai fi zis că Banco-ăla nici n-a existat vreodată. Ăştia da specialişti, nu ca prăpăditul acela brunet.

În timpurile alea televiziunile dormeau duse, sau doar moţăiau vizionând spoturile publicitare gen „Dormi liniştit, FNI veghează pentru tine”, marca Agenţia Tempo.

Oare cum se numeşte Drăghiciul din spatele acestor specialişti? Mare om! Mari specialişti, domnule!

Păi, ăia cu Marele jaf…, se zice că au ajuns în „livada cu pruni”, pe lângă Jilava, unde au înghiţit nişte sâmburi metalici. Cred că erau de 7,62. Sau mai ştiu eu ce pruni creşteau pe-acolo şi ce calibru aveau prunele de acolo.

Ăştia cu Bancorexul nimic. Meseria e brăţară de aur. Meseriaşii ăştia sunt de aur în întregime.

Până şi parcările s-au boschetat. Cum ajungi prin Dorobanţi, cum te invită un boschetar, sau boschetăreasă jegoasă sută la sută, să parchezi în locul pe care-l ţine sub observaţie.

Tot brunetă din alea de se spală cu şpaclul.
Odată la şapte ani.

Huo! Huo! Huo!
Blondo!
Păi aşa înţelegi tu să faci economie de piaţă? Aşa vrei matale să ne duci pe înaltele culmi ale capitalismului multilateral dezvoltat? Voi n-aţi auzit de bidinea? Puneţi mâna pe ea, trageţi nişte linii pe asfalt, faceţi-vă parcări ca la carte, şi apoi să-mi veniţi să-mi cereţi mie un leu pentru ora de parcare. Ce-i parcarea voastră? Nu vă e ruşine?

Bruneta cea blondă nici nu se sinchiseşte.
De unde s-a contaminat ea cu atâta nesimţire?

Ei, de unde?
De unde este.

Petrecere cu sertare

ElZap

În seara asta vă invit la o petrecere. Să zicem la o cafea. Ştiu că şi voi mă veţi invita la petrecerile pe care le organizaţi, mai ales că eu nici măcar nu sunt pretenţios. O cafea mi-e suficient.

Aţi sosit? Sunteţi toţi? Bun.

Văd că sunteţi 31 doamne şi 33 domni.
Aşezaţi-vă la masa mea rotundă.
Încercaţi să faceţi în aşa fel încât fiecare domn să aibă în faţa lui o doamnă.
Nu vă spun de ce.

Aţi reuşit?
Nu?

Mai discutăm.

Înmulţirea pâinilor

ElZap


Să nu se supere pe mine cuvioasele doamne, care o să-mi treacă pragul blogului, dar tot la cele sfinte o să fac trimitere şi în seara asta.

La înmulţirea pâinilor, desigur.

Că Iisus a reuşit să sature mulţimile cu doar cinci pâini şi doi peşti, asta am priceput-o, că doar şi eu trec pragul Sfintei Biserici. Şi nici nu erau puţini hămesiţi dintre cei ce veniseră să se sature. Evanghelia ne spune că erau cinci mii de bărbaţi. Pe atunci nu existau Drepturile Omului, necum Drepturile Femeilor şi ale copiilor, aşa că pe alea şi pe ăia nu i-au pus la socoteală Sfinţii Apostolii.

Am priceput, că doar ştiam că Iisus a făcut minuni.

Se zice că "au mâncat toţi şi s-au săturat şi au strâns rămăşiţele de fărâmituri, douăsprezece coşuri pline".

Mai aflăm din Cartea ce Sfântă că Iisus a dat din ale Sale. Din ale Sale, nu din pâinea celor săraci.

Aşa mai zic şi eu faptă bună.

Nu e ca la aleşii noştri, cei de toate zilele.

Se zice că şi ăştia ar fi dat ceva pâini, poate şi peşte, ulei şi şoşoni. Treaba e că ai noştri nu erau sfinţi, ca să înmulţească pâinile. Eu ştiu că pe al nostru nu-l cheamă Ilie Tesviteanul, ca să binecuvânteze uleiul şi făina văduvei din Sarepta Sidonului. Ba să-i mai învie şi copilul. Al nostru i-ar trage doar un dos de palmă. Aşa ca să vadă dacă mişcă.

Ai noştrii îşi înmulţesc doar pâinea lor, cea de toate zilele. Că aud că nu se mai satură, crăpa-le-ar burdihanul cel veşnic nesătul.

Atunci de unde au dat? Cât au dat? Cui au dat?
Toţi tac precum peştele. Ăla pe care l-au dosit, când trebuiau să-l dea mulţimilor. Au făcut jumi-juma cu gloata. Alt pezevenclâc.

Dar cu cele douăsprezece coşuri pline, cum s-a rezolvat?
Pline or fi ele, dar cu ce sunt pline? Aud că ar fi cu niscaiva datorii.
Pe alea cine le plăteşte? Nu cumva ăştia au făcut din timp nota de plată, pe care au înmânat-o tot mulţimilor?

Ba, eu cred că da.

Urâtă treabă.
Adică, părinţii mănâncă aguridă şi copiilor li se strepezesc dinţii.

Parcă numai copiilor?
Eu zic că şi nepoţilor, ba şi ...

Luându-mă după Ştefan, zic şi eu:

Democraţia n-a fost a strămoşilor mei, n-a fost a mea şi nu e a voastră, ci a urmaşilor voştri şa urmaşilor urmaşilor voştri în veacul vecilor...

Păi atunci să plătească urmaşii ăia, ce pana mea.
Eu acum am o treabă. O treabă ce nu suferă amânare. Colea, cu Răreşoaia.

Vreau şi eu un Petru Rareş, ca să-i las lui cheile împărăţiei, şi ce va lega pe pământ... Restul o să mă completeze cuvioasele.

Le-aş lăsa eu altcuiva, dar nu dai cheile unui care dă cu stângu-n dreptul.
Am avut eu grijă să exilez pe cei ce trebuie exilaţi.

Amin!

Doftore Şmil!
Doftore Şmil!
Eşti pe aproape? Când mă arzi? Cu flacăra aia violetă, cu care te tot lauzi.
Sau o lăsăm şi pe asta pentru urmaşi.

Că... eu pot să mă tratez şi la Viena.

Voodoo Aliodor

ElZap

Iar mi-a pierit somnul. Iar tresar din pat, de cum aţipesc. Pe sticlă îmi apare Voodoo. Voodoo Aliodor. Aliodor Manolea. Cel ce înalţă şi coboară preşedinţi. Pe mulţi îi aduce în pragul nebuniei.

Ăsta:



Geoaaaanăăăă, trezeşte-te!
Nu-l lăsa pe Aliodor să te biruie!

Te temi de flacăra violetă?
Teme-te, dar nu disperaaa....!
Flacăra asta o poţi învinge.
Dacă vrei poţi!



Ascultă-l pe Saint Germain!
Ascultă-mă pe mine!
Citeşte-l pe Harap Alb!
Îmbracă iute pielea cea de urs!
Aminteşte-ţi de Gerilă. Fă ca el!

Dacă poţi. Dacă nu poţi, e de rău.
Măcar angajeză şi tu un Gerilă, ca să-i stingă lui Roş Împărat flacăra cea violetă.

Păcat că n-ai reuşit să intri în pielea lui Elena. A lui Elena Udrea.
Dacă intri în pielea ei, poţi fi sigur că nici porţile Iadului nu te pot învinge.

Pe ea nu a învins-o nici comisia lui Orban, cât era el de liberal.
L-a privit odată scurt în ochi de i-a pâlpâit flacăra.



Pe urmă i-a aruncat în ochi două versuri de-ale lui Bolintineanu. Ascultă la ea, cât de bărbată a cuvântat:

— "Dacă nu ţi-e frică şi-ai credinţă-n tine,
O, tătare! vino sa te baţi cu mine!"

Mă rog, ea nu a zis chiar "O, tătare", că nu vroia să-l supere pe celălalt. A zis "O, Orbane", dar ce mai contează?

Contează că i-a trântit uşa-n nas, de au îngheţat pereţii, şi atunci flacăra cea violetă a lui Orban s-a stins pe vecie. S-a repezit apoi spre lift, şi i-a zis acestuia:

- Dii!

Liftul s-a conformat şi dusă a fost. Din flacăra lui violetă, nu au rămas nici tăciunii, ca să descânte de sperietură.

Trebuie să mă asculţi pe mine!

Trebuia...
Acum e târziu.

Dacă-ţi cântă cei de la PSD, priceasna de mai jos?
Aia cu... "Acum, slobozeşte pe robul Tău, Stăpâne, după cuvântul Tău, în pace, că văzură ochii mei mântuirea Ta."





Păi dacă ţi-o cântă ai feştelit-o!
Ai feştelito, Mircico!

Dar, lasă că tot răul spre bine. Vii şi tu aici la mine pe blog şi... ne scriem şi... ne cetim.

Scriem amintiri.
Amitiri din copilărie.


Doamne ajută!

Liliacul – zbor zigzagat

ElZap

Am căutat o fabulă de care mi-am amintit că o citisem pe când eram copil. Totdeauna îmi aduc aminte de astfel de poveşti taman când nu trebuie. Sau poate că... trebuie.

Se zice că un liliac a fost acostat în zbor de un uliu. Ce l-o fi apucat pe liliac să zboare ziua, chiar că nu pricep. Uliul pasămite era un fel de dăjdiar peste mulţimea păsărilor, şi nu concepea ca singur liliacul să scape de dări. Măcar cu un impozit forfetar şi tot trebuia să contribuie şi dumnealui la întreţinerea traseelor aeriene ale zburătoarelor. Zice-se că uliul vroia să planteze acolo în cer, nişte afişe pe care să scrie mare: aici sunt banii dumneavoastră. Domnişorul liliac (că se zice că nu avea mai mult de 23 de anişori pe-atunci) şi-a amintit însă că el nu este pasăre, ci un fel de şoricel cu aripi, aşa că a scăpat de bir, coborând iute pe pământ.

Numai că liliacul cel bicisnic, odată coborât printre ciulini, dă peste vulpe. Inutil să vă spun că şi vulpea era cam tot un fel perceptor peste cei de jos, şi că liliacul a trebuit să se dea din nou pasăre.

Nici acum nu s-a hotărât liliacul, ce este el de fapt, aşa că se comportă ca un fel de suveică între cer şi pământ.

Acum, ca să nu credeţi că mă ocup doar de lucruri neserioase, o să vă spun că m-am apucat de citit.

Întâi l-am citit pe domnul Urban Iulian, care-mi trimite zilnic nişte rapoarte de la cabinetul de senator al domniei sale, deşi eu nu-mi amintesc să i le fi cerut vreodată. Dacă mi le trimite eu le citesc. Aşa aflu eu despre:

Paradoxul lui Icar si Honorius
Paradoxul lui Icar s-a produs; PDL a suferit un esec dezastruos; Cine isi asuma infrangerea ? Batman, Batman….

De la domnul Urban, trec la HotNews, unde mă delectez cu o bucată de Dan Tapalaga. Mai precis cu bucata:

VIDEO Baiatu' lu' tata

O citesc şi pe asta. Buuuun.
Pe urmă trec pe YouTube, unde citesc ca miliţienii filmele. Adică pe ăsta:



De aici aflu că Honorius candidează pentru o funcţie în stat.
O fi.
A candidat.
A fost.
A zburat puiul cu aţa.

Deci de la mare distanţă aflăm că băiatul o să fie.

O să…

Pe urmă trec la Topârceanu. Ăla nu-l lasă în pace pe Minulescu. Îl parodiază în mod original.

Îl parodiază pe tema gramofonului. Ascultaţi numai. Cu ochii.

„Eu sunt un sarcofag de note îmbălsămate,
Un album
În care-o primadonă moartă
Dă
Gratis
Un concert postum.
Prin mine mor — ca să renască —
Vibraţii pentru mai târziu,
Eu sunt ce n-am fost niciodată
Şi-un sfert din ce era să fiu!”

Era bine dacă erai un sfert, nenicule.
Nu eşti.
Nici atâta.

Pe urmă mă opresc. De teamă.

Mi-e teamă de liliac.
Dacă descopăr că…

Mai ştii?

UPDATE:

Ştiri pentru care nu bag mâna în foc. De aia nici nu dau citate din locaţiile unde apar.

Honorius Prigoana are probleme cu diploma

Si-a terminat Honorius Prigoana studiile din SUA?

TV-net.ro - STIRI - A absolvit Honorius Prigoana Universitatea ...

Vasile Blaga: Honorius Prigoana este "varianta buna" aleasa de PDL ...

Emil Boc: Sunt convins că Honorius Prigoană va fi alegerea ...

Machiavelli.ro - Ştiri - Emil Boc: “Preda si Voinescu sunt noi in ... -

Aeroplanul de papură

ElZap

Demult, nici nu ştiu când, şi nici nu ştiu unde, am văzut un documentar cu un aeroplan făcut în întregime din papură.

Se pare că, în cel de-al doilea război, un avion a aterizat forţat pe o insulă nu tocmai pustie. Era locuită de un trib, ai cărui locuitori n-au văzut neam de neamul lor un avion sau aeroplan zburând. Impresionaţi însă de pasărea de oţel care a coborât din ceruri, ei s-au grăbit să construiască un fel de aeroplan din papură.

Se înţelege că aeroplanul ăla din papură nu a zburat niciodată. Nici nu avea cum.

Era doar un fel de reproducere a ceva ce „unii au văzut”, şi văzând li s-a părut că „au înţeles ce au văzut”. Cei drept, nici nemernicii aceia, care au violat spaţiul aerian al războinicilor locuitori ai insulei, n-au catadicsit să le explice cum trebuie procedat, pentru a face ca avionul lor să se înalţe. Ei şi-au luat avionul lor din oţel cu ei, l-au distrus, sau naiba ştie ce i-au făcut.

Nici măcar nu se ştie de ce au procedat aşa. Poate din grabă, poate din neglijenţă, sau poate pentru a nu cădea în mâinile locuitorilor un know-how extrem de preţios. Sau poate aveau tot interesul ca ăia să rămână la fel de înapoiaţi precum au fost găsiţi. Adică, tot în fundul gol, cum s-ar zice.

Mai trist decât povestea cu locuitorii acelei insule, este faptul că nimeni nu a tras vreo învăţătură cât de mică din acea întâmplare. Aproape nimeni.

Şi astăzi, după atâţia ani de la întâmplare îi vedem pe unii cum construiesc de zor, supersonice din papură, fără să se întrebe cum vine treaba cu industria aeronautică.

Unii o fac din prostie crasă, crezând că au priceput din prima cum trebuie meşterit un astfel de aeroplan. Nu pricep, dar o vreme ei sunt priviţi ca un fel de guru al insulelor peste care păstoresc. Se simt bine aşa, chiar dacă văd că aeroplanul rămâne la sol, precum o gâscă moartă. De cele mai multe ori îşi întemeiază un fel de dinastii locale, lăsând urmaşilor să gestioneze preţioasa lor înţelepciune. Başca influenţa dobândită. Şi cum să nu se simtă bine, dacă ei stau călare pe posturi grase de miniştri, prim-miniştri, ministrese, preşedinţi, sau dracu mai ştie cum le se spune. Se simt bine, nesimţiţii.

De cele mai multe ori însă, ei se comportă asemenea unor şefi de trib, practicând un fel de vânătoare sălbatică împotriva propriilor supuşi. Pe ei îi vând apoi ca sclavi unor negustori, veniţi de peste mări şi ţări. Supuşii sunt adunaţi ca să meşterească la pasărea lor de papură, iar când corabia a ancorat la mal, sunt împinşi spre o destinaţie imprevizibilă. Cam aşa au fost recoltaţi sclavii din continentul african, după cum puteţi constata dacă revedeţi filmul „Rădăcini” ( "Roots").

Astăzi cred că trebuie să fii atent şi la cei ce vin ca să te înveţe cum trebuie făcut un planor, că nu se ştie niciodată dacă nu cumva ei sunt doar un fel de popularizatori ai ştiinţei, pe care însă n-o posedă, sau şi mai rău, nişte indivizi care ţin morţiş să-ţi bage căruţa cu oiştea în gardul lor, ca să-ţi ia apoi şi căruţa. Căruţa ţi-o iau drept dobândă pentru cele trei surcele rupte din gard.

Măcar dacă am fi avut mintea cea de pe urmă, să ne fi învăţat din păţaniile altora.

Ba chiar din ale noastre.

Frământări

ElZap

Ce mă poate pe mine frământa în lipsă autoimpusă de cafea?

Păi, ar putea să mă frământe zaţul, adică... dacă iese sau nu iese Honorius.
Mă interesează, doar pentru a verifica nişte cugetări din popor.

Bunăoară, dacă tot e să se aleagă praful de Parlamentul României, de ce nu am pune şi noi în urnă votul cu Honorius ştampilat. Mai rău decât votul ăsta nu-i nici măcar TNT-ul.

După noi, Prigoană, că potopul este prea scump pentru vremurile astea de criză.

Şi apoi, ce mai contează dacă iese unul bun sau unul prost, atâta vreme cât ţara a mers binişor chiar fără guvern, câteva luni. Mai rău e să ai guvern, că unii de-acolo ar putea avea iniţiative.

Guvernanţii noştri ar trebui plătiţi, doar pentru timpul în care dorm, că dacă nu sforăie s-ar putea să nu ne facă rău. Nu este sigur.

Aşteptăm.
Aşteptăm să se anunnţe rezultatul.
Cam cum am aştepta să vedem ce păţim după ce ne cade ghilotina pe grumaz.

Mai vedem?

Băhăiala

ElZap

Mare zarvă prin ograda televiziunilor. Înclusiv prin ograda Realităţii. Aia prin care bate vântul de rupe frunzele. Vântul stârnit de o doamnă în costum adecvat, pe care o ştim doar după nume (Ioana Maria Vlas) şi după fond (FNI), că după chip nu prea suntem siguri.

Aflăm că, nişte locotenenţi ai unuia pe nume Sergiu Băhăian, ar fi ucis. Ar fi ucis cam mulţi. Vreo şapte. Cu cruzime. Cică e cam arestat.

Mare brânză. Parcă din arest nu se poate scăpa. Omar Hayssam a fost şi mai arestat. A fost şi mai păzit. A fost aproape mort. A fost, dar a scăpat de moarte. A scăpat el de toate. Aşa-i dacă ştii cum să înalţi rugăciuni fierbinţi "celui de sus".

La noi se vizionează filmul acela cu Omul care trece prin zid. Le passe-muraille. Cu Bourvil. Măcar să ne distrăm până la diversiunea următoare. Ţine doar zece minute.Filmul. "Următoarea" aia ar putea veni şi mai repede. Ăsta.



La noi toate zidurile sunt făcute din brânză. Prin brânza asta trec cei care pot. Nu încercaţi. Trebuie să aveţi spatele asigurat unde trebuie. Din brânza asta s-a făcut caşcavalul. La caşcaval se întind mulţi. Poezele. Poveşti de adormit copiii.

Eu nu cred că Sergiu ăsta stă prea mult. Doar atât cât să fie ocrotit. Nu se ştie niciodată cum reacţionează rudele morţilor. Morţii nu mai reacţioează. Pe urmă se mută procesul unde trebuie.

Parcă ar fi prima oară! Vă amintiţi de Virgil Săhleanu?
Sigur că vă amintiţi. Mort şi ăsta. Vorba lui Coşbuc.

-"Dar bietul Mircea?" -"Mort si Mircea,
Prin vai pe la Smardan."

Pe Mircea l-au ucis turcii. Erau în legitimă apărare. Mircea juca în deplasare.

Pe Virgil l-au ucis ai noştri. La ordin. Cică era unul, Frantisek Priplata, sau cam aşa ceva. Pri Plata ăsta juca el în deplasare. L-au purtat şi pe ăsta... L-au dus până hăăăt la Satu Mare. Ca să-l judece ca lumea. Acolo l-a scăpat pe jos. Pe jos, el a ajuns la graniţă. Mai avea de mers săracul cam... zece kilometri. A făcut un jogging scurt, care i-a dus libertatea mult visată.

La noi nu-i ca la Guantanamo. La noi e libertate. Cât pofteşti.

Să te ferească sfântul să fii în libertate. O poţi păţi scurt. Cel mai sigur e să fii după gratii. Ai acolo tot ce-ţi doreşti. Nu comentăm ce, că oricum e plină presa de poveşti. Oare doar poveşti?

Acum o să mă reculeg, tot cu versurile lui Coşbuc, gândind la faptul că noi trebuie să avem încredere în justiţie. Avem.

"Cu fruntea-n piept, ca o statuie,
Ca un Cristos bătut în cuie,
Ţinea privirile-n pământ,"

Şi noi le ţinem.
Eu le ţin de ruşine.

Ca la piaţă

ElZap

Când lucrurile se întâmplă în văzul lumii, tot omul este mai atent.
Bărbaţii se încheie la prohab, după ce ies de unde ies. Femeile au grijă să-şi aranjeze coafura proaspăt ciufulită, din varii motive.

Fiecare face în aşa fel ca să se vadă cât mai puţin, din ceea ce se întâmplă de altfel în mod natural.

Studii şi analize statistice complexe, bazate pe cele mai sofisticate metode, ne arată că omul (şi femeia desigur), ascund cam 90% din ceea ce li se întâmplă din cauza lor, sau din alte cauze. Mulţi ascund 100%, iar unii mai sofisticaţi ascund chiar 1000%.

Ce să mai crezi când lumea umblă în fundul gol, pe bulevard, sau pe la biserică, sau pe unde umblă ea? Păi, atunci înseamnă că treaba e groasă.Voi ce ziceţi?

Ce-ar fi dacă aţi vedea că vecinul vă cotrobăie prin casă, când vă întoarceţi de la serviciu, şi rămâne în continuare şi după ce ţi-ai pus ciorba în farfurie. Aţi spune că s-a obişnuit, cu meseria asta.

Hai să vedem însă cum "se rezolvă" un buget, de către aleşii noştri.




Nu vedeţi mai sus? No problem.

Intraţi mai jos.

http://webtv.realitatea.net/actual/teodor-melescanu-a-schimbat-scorul-unui-vot-din-parlament

Aşaaa....

min 00:27
Dacă numărăm pe bune, s-a dus dracului!
(Aşadar iese sau intră după cum vrem noi. Păi, nu tot aşa era şi pe vremuri? Era. Să mai aud eu că s-a schimbat ceva!)

min 00:29
Să ştii că trece dacă e pe bune.
(Totul e să ştii ce vrei. Vrei să treacă, e una. Nu vrei să treacă, e tot aia, dar cu alţi parametri.)

min 00:39
Hai, dă-mi voie să pun 138 ca să fie strâns.
(S-a făcut jupâne. Ne tocmim, cădem la pace şi iese ce vrem noi. Mulţi văd, puţini pricep.)

min 01:10
Pune şi tu mai mult să nu ne facem de tot rahatul, măcar vreo 45.
(Măcar de formă. Că trebuie să arate şi democraţia asta... puţin virgină... puţin cuvioasă... şi în rest ştiţi voi cum.)

Asta se întâmplă in public.

Ce se mai discută pe holuri, pe după colţ, pe la cârcium e uşor de înţeles.

Înmulţim cu 10, ca să corectăm cele 90 de procente.
Sau cu 100.

Adam Smith nu a primit premiul Nobel

ElZap

Acum el (Adam Smith) n-are nicio vină.

Vina o are altcineva. Poate o are un bebeluş moşit de două moaşe. De fapt de o moaşă şi un mamoş. Sesizez şi eu acest amănunt, că doar nu dau cu parul.

Aşadar, vine 13 ianuarie (2010 desigur). Vine cu Honorius călare pe Antenă. Pe Antena 2 desigur.

Cam pe-aici, dacă nu-i cu supărare:

http://www.antena2.tv/arhiva/vorbe-grele/2010-01-13

Buuuuun!

Oana Dobre întreabă (cam la min 10:45):
Cine-a fost Adam Smith?

Honorius (Prigoană, cum altfel):
Adam Smith a fost unul din cei mai mari economişti care a câştigat şi premiul Nobel în economie.

Nimeni nu suflă o vorbă. Nici Oana şi nici Victoraş.

Cum dracului să-l câştige, când Adam-ul ăsta a murit pe la 1790 după cum se poate constata din acte:

http://en.wikipedia.org/wiki/Adam_Smith

Nu l-a câştigat, nu pentru că nu-l merita. Nu l-a câştigat pentru că Nobel nu s-a grăbit să se nască. Nobel a fost mai leneş şi a venit pe lume prin 1833. Tot după acte:

http://en.wikipedia.org/wiki/Alfred_Nobel

Victor:

Pe partea economică, cum ar zice domnul Vangehlie ne-am descurcat.

(oare!?!!)

Cam pe la 15:45 se trezeşte şi Oana:

Adam Smith a trăit pe la 1790, cam pe-acolo. Am primit un SMS.

(Cam! Că atunci el a murit, şi pe urmă n-a mai trăit, după cum se poate deduce din context. Şi dacă nu primeai SMS-ul ăla? Îl lăsai pe Adam Smith în viaţă până în ziua de azi? Nu putea să moară sărmanul Adam, din cauză de SMS.)

Victor (împăciuitor):

Buuun! Nu Adam Smith îl face sau nu-l face parlamentar pe Honorius Prigoană .

(Nu! Dar cine-l face? Tot chestie de curiozitate. Aşa-s eu.)

Acum, stau şi eu şi mă mir.

Cum dracului ajung parlamentari nişte oameni ce încalecă secolele unul peste altul?

Aşa!

Şi presa?

La fel!

Am zis. Rămâneţi cu Marius!

Mi-e sete de repaus

Şi s-au mai rostogolit douăsprezece luni pe scările vremii, şi numărul de ani ce au trecut de la naşterea Lui a mai crescut cu unul.

Iar dacă la venirea Lui în lumea noastră, nici măcar o singură stea călăuzitoare nu a apărut pe cer, El a înălţat un Luceafăr pentru toţi cei ce doreau să-I urmeze.

El a creat o operă sine cera, la care nici un singur cuvânt nu trebuie adăugat, şi nici unul nu este de prisos, aşa că mi-e imposibil a vorbi despre El altfel decât prin propriile Lui cuvinte.

"În orice om o lume îşi face încercarea,
Bătrânul Demiurgos se opinteşte-n van;
În orice minte lumea îşi pune întrebarea
Din nou: de unde vine şi unde merge floarea
Dorinţelor obscure sădite în noian.

…

Când ştii că visu-acesta cu moartea se sfârşeşte,
Că-n urmă-ţi rămân toate astfel cum sunt, de dregi
Oricât ai drege-n lume - atunci te oboseşte
Eterna alergare... ş-un gând te-ademeneşte:
Că vis al morţii-eterne e viaţa lumii-ntregi."


“Căci unde-ajunge nu-i hotar,
Nici ochi spre a cunoaşte,
Şi vremea-ncearcă în zadar
Din goluri a se naşte.

Nu e nimic şi totuşi e
O sete care-l soarbe,
E un adânc asemene
Uitării celei oarbe.”



"În numele Celuia, al cărui vecinic nume
De a-l rosti nu-i vrednic un muritor pe lume,
Când limba-i neclintită la cumpenile vremei,
Toiagul meu s-atinge încet de vârful stemei
Regeşti, şi pentru dânsa te chem ­ dacă trăieşti
O, Sarmis, Sarmis, Sarmis! răsai de unde eşti."



- "Hyperion, ce din genuni
Răsai c-o-ntreagă lume,
Nu cere semne şi minuni
Care n-au chip şi nume;

Tu vrei un om să te socoţi,
Cu ei să te asameni?
Dar piară oamenii cu toţi,
S-ar naşte iarăşi oameni.

Ei numai doar durează-n vânt
Deşerte idealuri -
Când valuri află un mormânt,
Răsar în urmă valuri;

Ei doar au stele cu noroc
Şi prigoniri de soarte,
Noi nu avem nici timp, nici loc,
Şi nu cunoaştem moarte.

Din sânul vecinicului ieri
Trăieşte azi ce moare,
Un soare de s-ar stinge-n cer
S-aprinde iarăşi soare;

Părând pe veci a răsări,
Din urmă moartea-l paşte,
Căci toţi se nasc spre a muri
Şi mor spre a se naşte.

Iar tu, Hyperion, rămâi
Oriunde ai apune...
Cere-mi cuvântul meu de-ntâi -
Să-ţi dau înţelepciune?

Vrei să dau glas acelei guri,
Ca dup-a ei cântare
Să se ia munţii cu păduri
Şi insulele-n mare?

Vrei poate-n faptă să arăţi
Dreptate şi tărie?
Ţi-aş da pământul în bucăţi
Să-l faci împărăţie.

Îţi dau catarg lângă catarg,
Oştiri spre a străbate
Pământu-n lung şi marea-n larg,
Dar moartea nu se poate...

Şi pentru cine vrei să mori?
Întoarce-te, te-ndreaptă
Spre-acel pământ rătăcitor
Şi vezi ce te aşteaptă."

Invariantul (3) - Pecunia non olet

ElZap

Ziceam mai demult c-o să scriu despre un invariant din lumea noastră cea de toate zilele, deşi chiar şi invarianţii aritmetici au un gust aparte. Aparte, dar nu neapărat plăcut.

Ziceam, numai că… toate exemplele pe care le aveam în minte, parcă intraseră în pământ. Răutăcioşii ar putea spune că au tulit-o de frica împăratului din povestea lui Hans Christian Andersen. Ăla de umbla gol puşcă prin toată împărăţia lui. Alţii, la fel de răutăcioşi, ar putea spune că din cauza lu’ Roza, care-i mai vizitează pe oameni de la o anumită vârstă.

Doar pentru că nu vreau a-i lăsa în eroare pe răutăcioşii mei, trebuie să precizez că exemplele au plecat pe pustii doar de greaţă. O greaţă imensă, pe care nu o pot trata doar cu zeamă de lămâi, fie chiar şi pictate.

Norocul mi-a sărit de pe blog. De pe un anumit blog, de unde aflam ceea ce ştiam de multă vreme, şi anume că: „statuile postmortem nu ţin de foame-n timpul vieţii”.

Şi uite-aşa am ajuns la Vespasian (sau poate la Nero?!), care a spus, aşa cum se poate vedea în titlu, că banii n-au miros… Inutil să adaug, că el se referea la taxa pusă pe libertatea omului de a urina în voie.

Acum, mă întreb şi eu ca prostul: nu este asta o proprietate care nu se schimbă odată cu aplicarea unor transformări? Nu rămâne ăsta un invariant al schimbărilor de tot felul, al tuturor epocilor, o permanenţă a creaţiei umane aşezată ceva mai jos decât punctul în care parabola lichidă atinge cel mai de jos nivel?

Aş putea să fac săpături mai atente prin Wikipedia, să văd cine urina, în ce condiţii avea el voie s-o facă, etc. etc. etc. N-o fac, pentru că mă încăpăţânez să cred că este vorba de dreptul unor oameni avuţi, de a se descărca în capul altor oameni, care-şi doresc la rândul lor să fie şi ei avuţi. Cei din urmă, oameni cu talent mult (sau doar moderat, sau geniali, sau…), acceptau (pe vremea lui Vespasian, desigur) ca bogaţii de atunci să se umple de bucurie contra unei taxe modice.

Ce conta că produsul muncii lor avea miros. Erau băile publice, nu-i aşa? În cel mult câteva ceasuri erai curat ca înainte, şi o puteau lua de la capăt. Alţi bani, altă distracţie.

N-o să dau exemple, deşi ele nu lipsesc din peisajul istoriei.

Mă gândesc la numărul impresionant de indivizi pociţi, care au devenit frumoşi, numai pentru că nişte mânuitori de penel au acceptat jocul ăsta murdar?

Mă gândesc la scriitorii care şi-au murdărit pana, scriind imnuri de slavă unor indivizi care erau cel mult oameni ca fiecare din noi.

Mă gândesc la războaiele ce ne sunt cunoscute mai mult prin penelul unor pictori, sau prin pana unor scriitori, decât din relatarea rece a evenimentelor. Nu au ajuns unii domnitori să fie mari, după ce că şi-au băgat popoarele în belea, numai datorită faptului că a venit cohorta de artişti care a corectat ceea ce nu trebuia corectat?

Şi totuşi… În lumea reală niciun invariant nu este perfect. Nu e ca la aritmetică. Mai scapă câte o excepţie. Nu toate numerele sunt pare, sau impare, ca în textul de mai acu câteva zile. Au existat şi oameni „nepereche”.

Haşdeu spunea:

„În toate epocele au fost poeţi, pe care flămânda sărăcie, uneori numai deşertăciunea, pentru o ticăloasă pomană însoţită de o mai ticăloasă laudă, îi încovoia tămâitori dinaintea celor puternici. În toate epocele s-au văzut însă şi de acele firi semeţe, înalte, vrednice de solia ce le-a dat-o dumnezeirea, care niciodată n-au întins o mână cerşitoare către vreo mărire pământească…”

O fi având dreptate Haşdeu, dar Acela a fost unic. Poate va rămâne unic.

„Noi avem în veacul nostru acel soi ciudat de barzi,
Care-ncearcă prin poeme să devie cumularzi,
Închinând ale lor versuri la puternici, la cucoane,
Sunt cântaţi în cafenele şi fac zgomot în saloane;
Iar cărările vieţii fiind grele şi înguste,
Ei încearcă să le treacă prin protecţie de fuste,
Dedicând broşuri la dame a căror bărbaţi ei speră
C-ajungând cândva miniştri le-a deschide carieră. –”

Şi uite că se apropie 15 ianuarie, şi aşteptăm să auzim al treilea cântat al cocoşilor.

Până atunci, poeţii, pictorii, jurnaliştii de închiriat cu ziua sau cu campania electorală, se pot împlini în greutate, volum şi pungă. Ba chiar şi bloggerii cu ştaif, care îşi pot adăuga toate loazele în blogrolluri.

Înainte băieţi! Aveţi spatele asigurat.

La valoarea voastră, puteţi să vă puneţi pe blog până şi vecinele, soacrele sau concubinele amicilor.

Cu tot, cu verzele lor de tot râsul din coafură.

Peron

ElZap



Juan Perón. Preşedinte al Argentinei până în 1974.

Dar ce-a fi de spus despre el, când toată lumea îi cunoaşte biografia, inclusiv faptul că mormântul lui a fost profanat în 1987? Aproape nimic.

Dacă n-ar fi fost debarcat/suspendat în 1955, poate că ar fi avut mai multe mandate. Poate. Depinde cum e constituţia pe la ei. Dar aşa sunt oamenii. Nerecunoscători.

Norocul lui că a avut şansa de a reveni în fruntea statului în 1973. Nu pentru mult timp. Aşa-i viaţa.

Putea fi şi altfel? Sigur că putea. Istoria însă nu se scrie cu „poate” sau cu „dacă”. Asta este. Noi însă putem să scriem cum vrem. Noi nu scriem istorii.

Şi dacă Perón ar fi ajuta-o pe frumoasa dansatoare María Estela Martínez Cartas (Isabela Perón) să ajungă preşedintă ceva mai devreme? Sau măcar prim-ministru. De exemplu prin 1950. Cu puţină dibăcie, ea ar fi ajuns poate să fie iubită de argentinieni. Oamenii îşi schimbă ades părerile. Dansul, murăturile , sau împletitul ciorapilor e mult mai important în viaţa oamenilor decât s-ar putea crede.

S-ar fi căsătorit cu ea prin 1961, evident după ce ar fi divorţat de Eva Duarte. Oricum de Eva divorţase prin 1952.




Poate că Isabela Perón ar mai fi încă în preşedinta Argentinei. Poate că o vreme ar fi cântat într-un frumos duet, din opera „Jocul de-a preşedinţia”.

Şi ar fi trăit fericiţi până la adânci bătrâneţi. Nesupăraţi de moguli.

Invariantul (2)

ElZap

Acum, nu că ar fi nevoie să dăm o rezolvare problemei cu pomul minune, dar nu-i rău să scoatem la lumină invariantul ascuns în rezolvare.

Cei ce fac alergie la aritmetică, pot să sară peste deducţiile care urmează, deşi nu vom extrage nicio rădăcină pătrată, cubică sau de alt fel, ci cel mult nişte concluzii folositoare. Parcă, dacă n-aş fi spus că puteţi să săriţi, n-aţi fi putut s-o faceţi în voie?!

Dacă ne luăm după DEX ’98, acolo ni se spune despre invariant că el este o:

„mărime, relaţie, proprietate etc. care rămâne neschimbată în urma aplicării sau intervenţiei unei transformări.”

E clar ca lumina nopţii.

Să începem prin a reaminti enunţul problemei, că nimic nu ne costă să o copiem încă odată pe blog.

În pomul minune grădinarul a făcut să crească 25 banane şi 30 portocale. În fiecare zi el rupe două fructe şi în acelaşi timp în pom mai creşte un fruct. Dacă rupe două fructe de acelaşi fel atunci creşte o portocală, iar dacă rupe două fructe diferite atunci creşte o banană.

Care este ultimul fruct din acest pom minune şi de ce?

Înainte de a purcede la rezolvare, să observăm că la fiecare pas, culegătorul de fructe poate aplica una din următoarele trei „transformări”:

BB: Se iau din pom două banane, caz în care numărul de fructe scade cu o unitate. Mai precis dispar două banane şi apare o portocală (-2B+1P=-1F). Dacă numărul de banane a fost impar (aşa cum se şi întâmplă la început), el rămâne tot impar (25B-2B=23B; 17B-2B=15B; etc.).

PP: Se iau din pom două portocale. Şi acum numărul de fructe scade tot cu o unitate. Mai precis dispar două portocale şi apare o nouă portocală (-2P+1P=-1F). Treaba e că, numărul de banane nu se schimbă prin această transformare, aşa că… dacă el a fost impar, tot impar rămâne.

BP (sau dacă vreţi PB): Se iau din pom o banană şi o portocală. În pom creşte la loc o altă banană. Este evident că şi acum numărul de fructe scade cu o unitate, dar numărul de banane nemodificându-se el rămâne tot impar, dacă impar a fost.

Cum „transformările” de mai sus, pot fi puse în operă de către grădinar, cum are el chef, a ne apuca să socotim câte de-alea şi câte de celelalte au rămas în pom după fiecare zi, ar fi un adevărat calvar. Un milion de miliarde de miliarde de cazuri şi subcazuri.

Băgăm însă de seamă că:

după fiecare transformare numărul de banane rămâne impar.

Hopa! Asta-i bine. Adică oricum ar culege grădinarul fructe din pom, numărul de banane rămâne impar? Sigur că da.

Mai trebuie să observăm că, deşi în fiecare zi grădinarul ia din pom două fructe, numărul acestora scade exact cu o unitate. Scade precum nivelul de trai, după aplicarea unor măsuri de reformare a statului. Puţin dar sigur. Chiar riguros. De crescut nici vorbă, că nu ni se spune că s-ar pune mai mult de două fructe la loc. Aşadar vom avea pe rând 25+30=55; 54; 53; … fructe.

Atâta vreme cât în pom mai sunt cel puţin două fructe, este evident că grădinarul poate opera o transformare, deci nu se poate înţepeni mecanismul care aplică transformări. E un fel de jaf asigurat, ar zice unii. Cu alte cuvinte tot ajungem până la urmă la fundul satului. Asta spre bucuria noastră, sau a celor ce ne vor călca pe urme.

Doar când în pom rămâne un singur fruct, toată treaba se opreşte şi nouă nu ne rămâne decât să vedem ce fruct e cel ce a rămas în orango-bananierul nostru. Nu contează că acum socotim nimicul. Aşa am vrut-o, sau aşa a vrut grădinarul. Parcă mai contează. Ne reamintim că:

după fiecare transformare numărul de banane rămâne impar.

E clar că nu putem avea zero banane şi una portocală, că atunci numărul de banane ar fi par (zero este totuşi număr par, deşi nu-i clar cine cu cine se însoţeşte).

Aşadar în pom a rămas o singură banană, stingheră ca o cioară vopsită portocaliu.

Şi invariantul? Păi, invariantul este tocmai „proprietatea” în roşu, adică „numărul de banane este impar”.

Acum, noi am fi putut mânca liniştiţi banane sau portocale din pomul ăsta, chiar dacă habar n-aveam despre invarianţi, ba chiar am fi putut tăia pomul cu totul, precum a făcut Alexandru Macedon cu nodul gordian.

Ce am băgat eu de seamă în astă problemă e un lucru extrem de simplu.

În lumea în care trăim, de multe ori întâlnim lucruri importante, folositoare, periculoase, sau ziceţi-le cum vreţi dumneavoastră, ce nu ne sar în ochi de la început, dar care pot fi un fel de invarianţi roşii care şi-au schimbat doar culoarea.

Dacă de exemplu, întâlniţi un invariant lup, îmbrăcat în blană de oaie, ce faceţi? Nu folosiţi în mod eficient resursele pedestre, arma din dotare, sau cel puţin trageţi zăvorul după ce v-aţi închis în casă, având grijă ca el să rămână pe-afară?

Faceţi cum credeţi, dar să n-avem vorbe, şi să-mi spuneţi că n-aţi auzit de invarianţi.

Invariantul (1)

ElZap

… este un fel de “tot aia e”. Dacă nu e tot aia atunci nu e invariant. Simplu ca bună ziua, aşadar.

Invariantul însă poate fi şi el simplu sau complicat, în funcţie de problema concretă.

Bunăoară în aritmetica cea mai banală, dacă cineva ne pune să numărăm un cârd de gâşte, este la mintea cocoşului că o să ajungem la acelaşi rezultat oricum le-am număra. Numărul de gâşte din cârd se zice că este un invariant. Am putea număra şi un cârd de cocoşi, dar problema se simplifică nepermis de mult, din cauză că numărul lor este prea mic, dar mai ales pentru că ei sunt ţinuţi totdeauna în spatele găinilor. Asta numai dacă ele cântă pe bătătură.

Dacă luaţi o bucată de ciungam şi o mestecaţi, ea nu-şi modifică volumul oricât v-aţi chinui. Volumul bucăţii de Orbit este un invariant. Culoarea nu este, mai ales dacă sunteţi fumător înrăit sau dacă aţi băut o cafea.

După ştiinţa mea nu toate problemele sunt la fel de simple, precum e problema cu gâştele, sau cu guma de mestecat. Unele sunt chiar foarte complicate. Am putea lua pentru încălzire una pentru copii. O găsiţi şi pe net, desigur.

În pomul minune grădinarul a făcut să crească 25 banane şi 30 portocale. În fiecare zi el rupe două fructe şi în acelaşi timp în pom mai creşte un fruct. Dacă rupe două fructe de acelaşi fel atunci creşte o portocală, iar dacă rupe două fructe diferite atunci creşte o banană.

Care este ultimul fruct din acest pom minune şi de ce?

Este evident că aici şi-a băgat coada un invariant, şi nu este nicio îndoială că el v-a dat soluţia pe tavă.

Marea nenorocire cu invarianţii ăştia nu vine din aritmetică, sau din fizică. În lumea în care trăim, ne lovim la tot pasul de invarianţi.

Dacă nu mi se întâmplă nimic până data viitoare, despre acest soi de invarianţi aş vrea să scriu. Poate găsim unii interesanţi.

Cândva.

Zoo - iepuraşul

ElZap

Astăzi mi-a căzut din cutia de amintiri un banc. Bancul cu iepuraşul.

Iepuraşul acela viteaz, care doar stătea la margine de drum şi-şi făcea manichiura în mod ostentativ. Foarte ostentativ. De câte ori era întrebat de cei ce treceau fără treabă pe-acolo, de ce îşi ascute el unghiile cu atâta râvnă, el le răspundea ţâfnos:

- Voi chiar nu vedeţi că mă pregătesc să-l fac arşice pe leul cel ticălos? S-a terminat cu tirania leului.

Azi aşa, mâine la fel, până în ziua în care se prezintă la apel, chiar leul ţintă. Se înţelege că iepuraşul era ocupat cu manichiura, cu deontologiile, cu moralităţile - avea mai multe, pentru orice eventualitate - , cu discursurile, cu...

Credeţi că leul îl mai întreabă ceva în legătură cu ghearele sale? Aiurea! Nu-l întreabă nimic. Absolut nimic. Nu-l întreabă, însă iepuraşul pricepe. Pricepe că e cazul să-i dea un răspuns hazos, aşa că se execută.

- Mărite leu, uite, eu îmi fac manichiura şi… şi… şi… vorbesc prostii.

Cam aşa suna bancul ăsta ce mi-a căzut din cutia de amintiri. Bancul nu ne spune nimic despre soarta bietului iepuraş, aşa că putem să continuăm noi povestea, după cum ne duce mintea.

Eu, de exemplu, aş putea să-mi imaginez că leul s-a repezit la iepuraş, aşa din spirit de glumă. Poate chiar s-a oprit pentru o clipă deasupra lui, şi nici nu se ştie ce a făcut el, dar după ce a plecat leul, blana iepuraşului a rămas cafenie. Cafenie cu uşoare nuanţe de cacao. Unii spun că ar fi altă culoare.

Alţii ar putea să-şi imagineze, cum că iepuraşul a întrat într-o locantă, unde s-a apucat de filozofat, în faţa unui canceu cu vin roşu. Nu-şi mai făcea manichiura, ci medita la parastase şi la şpriţuirile de odinioară, timp în care amesteca puţin abătut cu o lingură… ceva în… altceva. Nu se ştie încă ce amesteca, în ce amesteca, dar bănuiesc că el ştie, dacă ar fi să mă iau după privire.

Pe urmă iepuraşul aprinde o ţigară, din care trage cu năduf, ca în vremuri de criză. Iepuraşul se pune pe scris. Îşi scrie un fel de autobiografie, ca să ştie cei ce ne-or călca pe urme, ce pericol a reprezentat el pentru leu. Asta dacă nu cumva se răzgândeşte domnul leu, de-l bagă sub o aripă, că în vremurile astea în care criza bate mai ceva decât codul portocaliu, poţi cumpăra ieftin un iepuraş flămând. Intri pe site-ul veveve punct totul redus punct ro şi dai sărci sau ţărci, că încă nu m-am lămurit.

În timp ce iepuraşul scrie, scrie, scrie… secundele se preling… ca în Dan Dănilă… sau ca în vremuri de criză. Poate morală.

„tot mai aproape furişate, parcă
auzi secundele foşnind în nisipar
şi noaptea bate cu aripi de ţarcă
desprinse chiar din negrul ei coşmar”

Secundele se preling, în timp ce o doamnă se străduieşte să pună un crin în glastră, care nu se ştie încă dacă e adormit sau ofilit de-a binelea. E singură, ca un fel de Ana Ipătescu, care nu se ştie ce căuta pe meterezele revoluţiunii de atunci. Poate doar ca să-i facă pârtie lui Dandanache, mare amator de coledzi. Că hodoronc-hodoronc, zdronca-zdronca..., nu-ţi faţi o idee, coniţa mea, nu-ţi faţi o idee, d-le prefect, neicusorule, nu-ţi faţi o idee, d-le prezident puicusorule...

Alţi iepuri, care nu s-au apucat să vorbească prostii la momentul nepotrivit, aleargă acum bezmetici de colo-colo ca să pună de ceva pentru un şoldan ce tot bezmetic aleargă pe autostrăzile patriei, care de fapt sunt nişte drumuri cu aspect de ogoare proaspăt arate. Aud că şoldanul ăsta a rămas fără permis, după ce a alergat fără permis cu viteza pe care o ştiţi. Păi dacă a rămas fără el, după ce că nici nu-l avea, cum o să conducă el? Eu cred că la fel. Fără carnet, fără aia, fără aialaltă, adică aşa de-a-n boulea, cum scrie la DOOM. Ca doamna mamă, de exemplu.

Şi dacă tot am vorbit de iepuraşi, de ce să nu ne gândim la cei ce-şi vor închide electronicele cutii poştale, vor trece pe trotuarul de vizavi al blogului, doar ca să nu-i noteze leul în cartea lui cea neagră.

Aşa-i în vremuri de criză. Mai ales de aia morală.

Aştept răspuns.
Post-restant.
Că nu se ştie niciodată ce aduce anul.