ElZap

Un parc cu alei. Ca cele din figura de mai sus. Simplu.
Dacă vreţi putem să le dăm şi nume vârfurilor dreptunghiului. A, B, C, D. Începând din coltul stânga sus. Mergem după cum merg acele ceasornicului. Putem să-i dăm centrului numele O.
Lăţimea dreptunghiului: 6 metri.
Lungimea dreptunghiului: 8 metri.
Lungimea diagonalelor? Inutil să spun. Evident 10 metri. Din cauză de Pitagora.
Câte cinci metri de fiecare parte a centrului.
Un paznic. Rolul lui? În fiecare zi să inspecteze aleile metru cu metru.Nu trebuie să lase nimic neinspectat.
El poate începe din oricare colţ. Dacă vrea poate începe şi din centru.
El ar vrea să parcurgă un traseu cât mai scurt. Nu are voie să ţopăie dintr-un colţ în altul. Poate termina oriunde.
Cam câţi metri are de inspectat paznicul zilnic?
Explicaţiile se impun.
UPDATE:
Un desen mai acătării:

REZOLVARE (PROGRESIVĂ):
R1:
Dacă o figură este formată din "insule" (ca în exemplul de mai jos) paznicul nu poate parcurge/inspecta toate aleile în niciun fel.

(De la A la E nu pot ajunge decât cu elicopterul.)
Urmează R2.
INTERMEZZO
Pentru acei copii mari sau mici care nu au obosit să se joace cu creionul pe hârtie.
Cine ştie ce drăcie mai poate ieşi din jocul ăsta?
R2:
Să presupunem de acum încolo că reţeaua de alei nu are insule ca în exemplul de mai sus, aşa că paznicul o poate inspecta fără bătaie de cap. Este şi cazul cu reţeaua din problema noastră.
Să zicem că îi cerem paznicului să facă în aşa fel încât să nu treacă de două ori pe o alee.
Dacă paznicul pleacă din intersecţia X şi termină inspecţia în intersecţia Y, o să vedem că pentru orice intersecţie Z, alta decât cele două X, Y numărul de alei ce se întâlnesc în Z este par. Asta din cauză că pe o alee a intrat şi pe una a ieşit din Z (le poate şterge din desen dacă vrea, ca să nu ne mai încurce la socoteli), şi nu a rămas nicio alee neparcursă care să fie vecină cu Z.
Pentru punctele de start şi stop X, Y, vom avea un număr impar de alei ce se întâlnesc în ele dacă ele sunt diferite, sau un număr par dacă sunt identice.
În concluzie:
Dacă numărul de intersecţii cu un număr impar de alei adiacente, este diferit de 2 sau 0, nu poate nimeni să parcurgă reţeaua trecând doar odată pe fiecare alee.
Este şi cazul reţelei noastre ce are 4 intersecţii impare. Prin urmare cade posibilitatea ca paznicul să parcurgă reţeaua în 48 de metri.
Exemplul 1
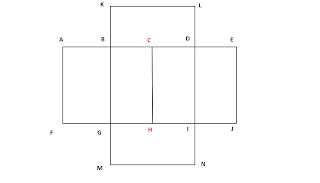
În acest exemplu aleile pot fi parcurse o singură dată, numai dacă pornim din unul din punctele C sau H.
Exemplul 2

În acest exemplu aleile pot fi parcurse o singură dată, pornind din oricare din punctele rețelei.
Exemplul 3

Nu există posibilitatea de a parcurge rețeaua o singură dată din cauză că am 4 puncte ce au un număr impar de alei adiacente.
Ar mai trebui să demonstrăm că în situaţia în care o reţea de alei are 0 sau 2 intersecţii cu un număr impar de alei care intră/ies din ele, totdeauna putem inspecta aleile trecând o singură dată pe fiecare alee. În plus, punctul de plecare se află în intersecţiile impare (dacă sunt două) sau într-o intersecţie arbitrară dacă sunt 0 intersecţii impare.
R3:



Cum rețeaua din problemă nu poate fi parcursă trecând o singură dată pe fiecare alee, caz în care paznicul ar avea de parcurs 48 de metri, suntem obligați să permitem paznicului să treacă de cel puțin două ori pe una sau mai multe alei.
Este evident că a-i permite să treacă de două ori pe o alee este echivalent cu a înlocui o alee cu două identice (a o dubla). Încercăm să dublăm aleile de 5m, 6m, 8m, ca în figura alăturată.
Dublarea aleii de 5 metri nu permite parcurgerea rețelei pentru că avem patru intersecții impare (A, C, D, O). Așadar nu putem avea un traseu de 48+5=53 metri.
Putem dubla oricare din aleile de 6 metri (o putem face în două moduri), sau de 8 metri (la fel o putem face în două moduri).
Evident, o vom alege pe cea de 6.
În acest caz obținem un traseu de 48+6=54 metri.
Răspuns corect
Paznicul trebuie să parcurgă zilnic 54 de metri.
Prima care a dat un răspuns corect, fără să ne ajute însă cu o motivație, a fost

Un parc cu alei. Ca cele din figura de mai sus. Simplu.
Dacă vreţi putem să le dăm şi nume vârfurilor dreptunghiului. A, B, C, D. Începând din coltul stânga sus. Mergem după cum merg acele ceasornicului. Putem să-i dăm centrului numele O.
Lăţimea dreptunghiului: 6 metri.
Lungimea dreptunghiului: 8 metri.
Lungimea diagonalelor? Inutil să spun. Evident 10 metri. Din cauză de Pitagora.
Câte cinci metri de fiecare parte a centrului.
Un paznic. Rolul lui? În fiecare zi să inspecteze aleile metru cu metru.Nu trebuie să lase nimic neinspectat.
El poate începe din oricare colţ. Dacă vrea poate începe şi din centru.
El ar vrea să parcurgă un traseu cât mai scurt. Nu are voie să ţopăie dintr-un colţ în altul. Poate termina oriunde.
Cam câţi metri are de inspectat paznicul zilnic?
Explicaţiile se impun.
UPDATE:
Un desen mai acătării:

REZOLVARE (PROGRESIVĂ):
R1:
Dacă o figură este formată din "insule" (ca în exemplul de mai jos) paznicul nu poate parcurge/inspecta toate aleile în niciun fel.

(De la A la E nu pot ajunge decât cu elicopterul.)
Urmează R2.
INTERMEZZO
Pentru acei copii mari sau mici care nu au obosit să se joace cu creionul pe hârtie.
Cine ştie ce drăcie mai poate ieşi din jocul ăsta?
R2:
Să presupunem de acum încolo că reţeaua de alei nu are insule ca în exemplul de mai sus, aşa că paznicul o poate inspecta fără bătaie de cap. Este şi cazul cu reţeaua din problema noastră.
Să zicem că îi cerem paznicului să facă în aşa fel încât să nu treacă de două ori pe o alee.
Dacă paznicul pleacă din intersecţia X şi termină inspecţia în intersecţia Y, o să vedem că pentru orice intersecţie Z, alta decât cele două X, Y numărul de alei ce se întâlnesc în Z este par. Asta din cauză că pe o alee a intrat şi pe una a ieşit din Z (le poate şterge din desen dacă vrea, ca să nu ne mai încurce la socoteli), şi nu a rămas nicio alee neparcursă care să fie vecină cu Z.
Pentru punctele de start şi stop X, Y, vom avea un număr impar de alei ce se întâlnesc în ele dacă ele sunt diferite, sau un număr par dacă sunt identice.
În concluzie:
Dacă numărul de intersecţii cu un număr impar de alei adiacente, este diferit de 2 sau 0, nu poate nimeni să parcurgă reţeaua trecând doar odată pe fiecare alee.
Este şi cazul reţelei noastre ce are 4 intersecţii impare. Prin urmare cade posibilitatea ca paznicul să parcurgă reţeaua în 48 de metri.
Exemplul 1

În acest exemplu aleile pot fi parcurse o singură dată, numai dacă pornim din unul din punctele C sau H.
Exemplul 2

În acest exemplu aleile pot fi parcurse o singură dată, pornind din oricare din punctele rețelei.
Exemplul 3

Nu există posibilitatea de a parcurge rețeaua o singură dată din cauză că am 4 puncte ce au un număr impar de alei adiacente.
Ar mai trebui să demonstrăm că în situaţia în care o reţea de alei are 0 sau 2 intersecţii cu un număr impar de alei care intră/ies din ele, totdeauna putem inspecta aleile trecând o singură dată pe fiecare alee. În plus, punctul de plecare se află în intersecţiile impare (dacă sunt două) sau într-o intersecţie arbitrară dacă sunt 0 intersecţii impare.
R3:



Cum rețeaua din problemă nu poate fi parcursă trecând o singură dată pe fiecare alee, caz în care paznicul ar avea de parcurs 48 de metri, suntem obligați să permitem paznicului să treacă de cel puțin două ori pe una sau mai multe alei.
Este evident că a-i permite să treacă de două ori pe o alee este echivalent cu a înlocui o alee cu două identice (a o dubla). Încercăm să dublăm aleile de 5m, 6m, 8m, ca în figura alăturată.
Dublarea aleii de 5 metri nu permite parcurgerea rețelei pentru că avem patru intersecții impare (A, C, D, O). Așadar nu putem avea un traseu de 48+5=53 metri.
Putem dubla oricare din aleile de 6 metri (o putem face în două moduri), sau de 8 metri (la fel o putem face în două moduri).
Evident, o vom alege pe cea de 6.
În acest caz obținem un traseu de 48+6=54 metri.
Răspuns corect
Paznicul trebuie să parcurgă zilnic 54 de metri.
Prima care a dat un răspuns corect, fără să ne ajute însă cu o motivație, a fost
INA.
Felicitări!









Niciodata destui!:))
RăspundețiȘtergereBuna dimineata!
klaus
Redevenind serios: 48m.
RăspundețiȘtergereklaus
@klaus
RăspundețiȘtergereSigur? Vezi cum i-ar face cei 48!
El nu are voie să țopăie din colț în colț ca un iepuraș.
(Mergi cu creionul pe traseu și nu ridica vârful creionului de pe hârtie.)
Are voie să treacă de două ori pe aceeaşi alee?
RăspundețiȘtergereDacă nu, nu ştiu...
Dacă da, atunci cred că cel mai scurt traseu are 53m, undeva trebuie să se întoarcă din drum 5 m, jumate de diagonală, ca să închidă "pliculeţul" :)
E doar o presupunere.
Probabil că soluţia ideală e cu 48 de m, dar eu n-o văd...
@renata
RăspundețiȘtergereAre voie!
Ești sigură? Dacă da, zi-mi și mie traseul.
Exemplu:
A-B-?-...
ElZap, credeam că tu deja îl ştii!
RăspundețiȘtergereFiindcă eu încă nu l-am descoperit.
@renata
RăspundețiȘtergerePăi, eu ştiu rezolvarea. Dacă tu zici că poţi să-l îndrumi pe un rum de 53 ar trebui să-l instruim şi cum ar trebui să meargă pe acel drum.
Pe paznic.
Nu pot şi pace!
RăspundețiȘtergereŞtiu că, dacă am reuşit de câteva ori repetând drumul pe latura de 6m, se poate şi pe o variantă unde revii pe cea mai scurtă, de 5.
Dar nu mă duce capul, zău!
E tot atât de incitantă ca problema aia, cu cei X oameni care se deplasează pe un podeţ cu viteze diferite ...ah! Aia era tare de tot! Dar n-o mai ştiu :)
RăspundețiȘtergereÎntotdeauna cel care putea merge mai repede se plia pe viteza celui care merge mai încet. Ţi-o aminteşti?
@renata
RăspundețiȘtergereAcum nu mi-o amintesc, dar mă strădui.
Mă întreb cum ai reuşit să mergi de două ori pe latura de cinci (OA, OB, etc.)?
Dacă zici că ai reuşit, aş vrea să o văd.
Ceva ai observat pe-acolo şi ai observat bine.
54m, trei variante cu repetarea unei laturi de 6m.
RăspundețiȘtergereAtit ma duce pe mine capul.
ADCBAOCBOD
ADOCBAOBCD
ADOBCOABCD
Eu doar de-atit sint in stare. Mersi pentru intelegere.
ElZap,
RăspundețiȘtergereEra un fel de joc-problemă. Nişte tipi trebuiau să parcurgă o punte cu o lumânare, felinar, care ţinea numai "n" minute sau secunde. Unul trebuia să ducă mereu felinarul de pe un mal pe celălalt, ca la o ştafetă şi nu puteau trece decât câte doi deodată. Trebuia să-i treci pe toţi, în intervalul cât ardea lumina, respectând timpii individuali de deplasare.
Nici acum nu-ţi aminteşti?!
@Ina
RăspundețiȘtergereMult mai aproape de rezultat!
Acum, ar trebui să lămureşti de ce nu s-ar putea cu 53 de metri, parcurgând latura de 5 m de două ori, sau de ce nu chiar 48, fără a parcurge nimic de două ori?
@renata
RăspundețiȘtergerePăi dacă nici tu nu ţi-o aminteşti...
Să nu ne pierdem speranţa.
@renata
RăspundețiȘtergereDupă ce o rezolvăm pe asta o aduc și pe aia cu podurile. E interesantă.
Poate și altele.
ElZap, nu intinde coarda :)))
RăspundețiȘtergere@Ina
RăspundețiȘtergereAșa zic și eu, dar...
De unde pot ști eu că mâine nu apare klaus cu soluția de 48m. Nimeni nu a dovedit că nu există o astfel de soluție.
Sau renata, care ne amenință cu soluția de 53 de metri.
Eu aș vrea să-ți dau ție dreptate, numai că trebuie să ți-o iei.
Așa că... mai am răbdare să se limpezească problema.
Se subînțelege că inspecția cea mai scurtă este cea corectă.
Vezi, ElZap?
RăspundețiȘtergereO soluţie oficială se impune!
@renata
RăspundețiȘtergereOficială? Şi atunci ce facem? Încălcăm drepturile vizitatorilor de a-şi încerca norocul?
Poate găseşte cineva o soluţie mai bună decât Ina!?!
Adică una în care paznicul parcurge un drum mai scurt.
Cum vrei, ElZap!
RăspundețiȘtergereProblemele nesoluţionate ne sunt probleme.
Încă!...
@renata
RăspundețiȘtergereUmila problemă de mai sus este departe de a fi foarte complicată şi cu atât mai mult nu poate fi una nesoluţionată.
Treaba e că sunt nenumărate probleme care rămân probleme nesoluţionate, dar asta-i o altă problemă.
Uite o problemă care nu este rezolvată de câteva sute de ani:
Două numere prime se numesc gemene dacă diferenţa lor este egală cu 2.
Exemple: (3, 5), (11,13), (29,31),...
Câte numere prime gemene există?
Există o infinitate de numere prime?
Pentru a găsi numere prime in ce în ce mai mari au fost puse în mişcare reţele de calculatoare inimaginabile ca putere de calcul.
Culmea e că sunt astfel de probleme în foarte multe domenii.
http://en.wikipedia.org/wiki/PrimeGrid
NU ştiu...
RăspundețiȘtergereCă pentru a găsi numere prime de tipul 29-31 s-au pus la muncă mai calculatoare, mi se pare firesc.
Dar în problema parcului, paznicul... va face zilnic drumurile astea, ocolind inutil, până ce, într-o zi, va descoperi singur, cu pasul, traseul cel mai scurt, plătit la fel fiind, de municipalitate.
Numai că nu va genera niciodată un tratat ştiinţific, unde să explice, băi, dacă aveţi de inspectat o parcelă cu dimensiunile... , cu x alei de acces , să ştiţi că ăsta e drumul cel mai scurt!
Vreau să zic că dă-ne soluţia, fiindcă CELĂLALT răspuns, e că paznicul va urma întotdeauna traseul cu care s-a obişnuit, acestuia părându-i cel mai scurt.
Deja miroase a ars din bucătărie! :))
@renata
RăspundețiȘtergereUite că am ajuns la Königsberg (mă rog, acum se numeşte altfel). Un fel de paznic, pe numele Euler se tot plimba aiurea peste nişte poduri.
Şi el se întreba dacă nu cumva ar putea să facă în aşa fel încât să nu treacă decât o singură data pe fiecare pod.
http://en.wikipedia.org/wiki/Seven_Bridges_of_K%C3%B6nigsberg
Problemuţa asta a ajuns să facă o teorie. (Teoria grafurilor euleriene).
Cam de aici se trage şi problema noastră.
Numai că nu aspiră la gloria lui Euler.
http://en.wikipedia.org/wiki/Leonhard_Euler
De scris, a scris omul ăsta de nu apuc eu să citesc în câteva vieţi.
http://books.google.com/books?lr=&cd=9&as_brr=1&q=inauthor%3A%22Leonhard+Euler%22&btnG=Search+Books
:))
RăspundețiȘtergereElZap, mi-ai distrus intreaga dimineata! Liber fiind, am zis sa-ti urmez sfatul, ala cu plimbatul creionului pe hartie. Daca mai tin bine minte, cel mai scurt n-am reusit sa-l scot sub 53. Am elaborat insa, o intreaga teorie despre puncte in care se unesc doua sau trei drepte :)).
Oricum, nu ma las!
Multzam prietene, mi-ai readus aminte de momentele in care ,,disperam'', uneori si timp de cateva saptamani, dupa solutia unei probleme sau cuvant(rebus).
De mai scurtez, macar cu juma' de metru :)), periplul paznicului iti voi da de stire.
klaus
@amicul klaus
RăspundețiȘtergereNici nu ştii ce m-a impresionat postarea ta.
Păi asta înseamnă mult, tare mult.
Dacă am reuşit să te pun să te joci "cu creionul pe hârtie", înseamnă că problemuţa asta nu-i chiar de lepădat.
Din fericire sau nefericire (ia-o cum vrei), lucrul ăsta mă determină să mă opresc o ţâră din a publica restul de paşi care duc la rezolvare. Doar din cauza ta şi a celor care mai scotocesc la o soluţie.
Eu chiar cred că cineva ar putea găsi o soluţie dreaptă la năsărâmba asta. Poate mult mai bună decâte cea pe care o am eu în cap.
ElZap,
RăspundețiȘtergeremie îmi datorezi 6 coli de hârtie faţă-verso şi un creion Hardtmuth 4B, plus toate farfuriile şi ceştile lăsate nespălate în prima zi în care ai lansat problema. Mi-am zdrelit creierii fără folos, însă.
Acum, timp de juma de oră, o mai iau odată de la capăt. Calmă. Fără idei preconcepute. Pe urmă, mă predau.
@renata
RăspundețiȘtergereDoar atât?
(Era cât pe-aci să șterg postarea cu totul.)
Când eram mic îmi cupăram câte un top de caiete maculator. De la 10 în sus. Le terminam într-o săptămână.
Răsplata? Dreptul de a chiuli de la ce vroiam eu. Și am chiulit. Mai ales de la Română.
Nu-mi pare rău.
Da. Doar atât.
RăspundețiȘtergereCred că singura variantă posibilă practic e aia cu trecutul de două ori pe latura de 6m.
Adică AOCDOBCBAD
Egal 54 de metri.
Cu o variantă în oglindă, unde dublează drumul pe AD-DA
Vrea domnul paznic aşa? Bine. NU, trimite-l să inspecteze poduri în Konigsberg.
@renata
RăspundețiȘtergereCu 54 sau cu 53...
Depinde ce dublezi.
Pot dubla și OD?!
Habar n-am. Deocamdata.
Am impresia că tu vrei să ne înveţi încet-încet, matematică!
RăspundețiȘtergereEu trebuie să chiulesc, deja! :)
@renata
RăspundețiȘtergereNuuuuu! Mai ales că nici eu nu o știu.
Am şi eu o problemă pentru tine, ElZap!
RăspundețiȘtergereNici n-are treabă cu matematica.
Aranjează rândurile de mai jos după un plan de simetrie, fără să muţi semne grafice de pe un rând pe altul. O să obţii o imagine. Să zicem reprezentarea grafică, stilizată , a unui obiect despre care se face vorbire undeva, în cuprinsul postului tău. :))
*O*
¤==(M)==¤
III
WWW
wwwwwww
II II
o o
@renata
RăspundețiȘtergereMuţumesc. Pornesc la atac asupra obiectului. Iese bine, nu iese mă dau bătut.
@renata
RăspundețiȘtergerePână aranjăm temeinic liniile astea îţi las şi eu jocul la care faci referire mai sus (1 februarie 2010, 21:34).
Ăsta este.
http://www.learn4good.com/games/puzzle/the_bridge.htm
Ah, dar nu-l voiam doar pentru mine!
RăspundețiȘtergerePentru toţi prietenii tăi.
Pentru Ina şi klaus...
Nu-l poţi posta ca problemă?
Fiindcă eu mă voi juca cu el pe cont propriu, foarte cinstit. Am uitat soluţia.
@renata
RăspundețiȘtergereO să văd ce fac cu el în următoarea postare.
La comentarii, în mod sigur nu.
Să se termine cu paznicul şi vedem.
Pentru toţi amicii mei desigur.
Îl iau de aici, deocanmdată.
Sau din academie.
Pot să depun o contestaţie, ElZap?
RăspundețiȘtergereNu, glumeam!
Acum, în mod normal, ar trebui să-i faci Inei un cadou.
Nişte flori, un cântec... ştii tu, te pricepi!
Sau... o problemă şi mai grea! :)))
@renata
RăspundețiȘtergerePoți, și chiar mă gândesc la un cadou adecvat.
De alltfel nu numai INA a intuit răspunsul corect ci și renata și klaus.
Ina a dat și niște trasee.Pe toate nu putea să le dea pentru că sunt enorm de multe. Pot dubla AD sau BC, iar apoi pot să mă plimb ca mai știu eu cine pe alei.
Ina a lăsat să se înțelegă că știe de ce soluția ei este bună, dar nici până azi nu m-a dumirit.
Nu este adevarat! Nu am lasat sa se inteleaga asa ceva! Pentru ca stiu ca e foarte complicata explicatia- de altfel am incercat sa urmaresc demonstratia ta si nu am reusit. Sint notiuni de mult uitate, nu mai reusesc sa le inteleg.
RăspundețiȘtergerePovestea cu podurile mi-o amintesc, profesoara mea de mate ne-a aratat-o la un "cerc de mate", ca pe o curiozitate. Avea si o explicatie foarte complicata pentru care parcurgerea podurilor alora o singura data e imposibila- bineinteles ca nu am retinut explicatia.
Nu te baza pe mine pentru demonstratii, te rog. Nici vorba!!!Nu, nu , nuuuuuu!!!
Renata, esti draguta sa te abtii de la sugestii de cadouri? :)))
@Ina
RăspundețiȘtergereUite că mi-am amintit eu ce ţi-a zis profesoara la cercul ăla.
Şi m-am grăbit să o pun aici. Dacă ţii minte doar ce e scris cu roşu e bine. Demonstraţia e simplă. Între o ciorbă şi o friptură ai tot timpul să o înţelegi.
Unii ar zice că e caraghos de simplă.
Nici n-am vrut să fie altfel.